QUESTÕES
Petrobras
2010
62
Considere o problema abaixo de
Programação Linear.
Minimize: Z = α.X1 + β.X2
Para quais valores de α e β o problema apresenta soluções múltiplas?
(A) α = 2 e β = 4 (B) α = 2 e β = 1 (C) α = 1 e β = 1 (D) α = 2 e β = 3 (E) α = 3 e β = 3
Resolução
Programação linear se baseia em linhas, isto é,
em retas. A função objetivo e as restrições são retas. Para haver múltiplas
soluções, a função objetivo deve ser paralela a alguma das restrições (sempre
se lembrar disso, cai bastante). E como é o paralelismo de retas? Quando seus
coeficientes são múltiplos um do outro. Neste caso, só temos uma reta de
restrição X1 + 2X2 > 9. Então, α e β devem ser
múltiplos dos coeficientes da restrição (1 e 2), podem ser 1 e 2 (se
multiplicados por 1), 2 e 4 (quando multiplicados por 2), 3 e 6 (se vezes 3) e
assim por diante. A alternativa que apresenta múltiplos é alt A.
2011
67
Considere o seguinte problema
de Programação Linear.
Min Z = 2x1− x2
Sujeito a
−x1 + x2 ≤ 3
2x1 − x2 ≤ 6
x1 ≥ 0
x2 ≥ 0
Qual é a solução ótima?
(A) x1 = 0 e x2 = 1 (B) x1 = 0 e x2 = 3 (C) x1 = 1 e x2 = 0 (D) x1 = 1 e x2 = 4 (E ) x1 = 3 e x2 = 0
Resolução
A melhor maneira de resolver é substituindo cada
uma das alternativas e achar a solução ótima. Detalhe que ele quer MINIMIZAR o
Z, então, a solução ótima é a menor. Letra A (0,1) Z= 2.0-1= -1. Letra B (0,3)
Z= 2.0-3= -3. Letra C (1,0) Z= 2.1-0= 2. Letra D (1,4) Z= 2.1-4 = -2. Letra E
(3,0) Z = 2.3-0 = 6. O menor valor de Z é -3 da alt B.
68
Considere o problema abaixo de
Programação Linear.
Maximize: Z = −3*X1 + 6*X2
Sujeito a:
X1 ≥ 0
X2 ≥ 0
5* X1 + 7*X2 ≤ 35
α* X1 + 2*X2 ≤ 2
Para qual valor de α o problema
apresenta soluções múltiplas?
(A) α = −1 (B) α = −0,5 (C) α = 0 (D) α = 0,5 (E) α = 1
Resolução
Novamente “soluções
múltiplas”. Soluções múltiplas acontecem quando a reta da função objetivo é
paralela a reta de alguma das restrições. O paralelismo entre retas se
caracteriza pela multiplicação dos coeficientes. A questão pede o valor de α,
então essa equação é múltipla da função objetivo. Para o 6 de X2 “virar”
2 na restrição, foi dividida por 3. Fazendo o mesmo para o coeficiente -3 de X1:
α= -3/3 = -1. Alt A.
2012
68
Considere o seguinte problema
de programação linear:
Maximize: Z = 3x1 + 7x2 + 5x3
Sujeito a
x1 + x2 + x3≤5
2x1 + 3x2 + x3≤10
x1≥0
x2≥0
x3≥0
Qual o valor máximo que o
coeficiente da função objetivo para a variável X1 pode assumir, sem alterar a
solução ótima do problema de programação linear apresentado?
(A) 3 (B) 4 (C)
6 (D) 7 (E) 8
Resolução (dos comentários)
Na questão 68 não precisa usar o dual e não é através da proporção entre as variáveis.
Uma técnica utilizada e "zerar" a variável envolvida.
Fazendo x1=0
Z= 7X2 + 5X3
s.a
X2+x3<=5
3X2 + X3 <=10
Resolvendo pelo método gráfico, encontramos (2,5 , 2,5)
Então
Z= 3*0 + 7*2,5 + 5*2,5 = 30
Quando mudamos o valor do coeficiente de X1 na FO chega uma hora em que ficará mais vantajoso produzir apenas X1.
Zerando X2 e X3 (5,0,0)
30 = Alfa*5 + 7*0 + 5*0
Alfa = 6
Uma técnica utilizada e "zerar" a variável envolvida.
Fazendo x1=0
Z= 7X2 + 5X3
s.a
X2+x3<=5
3X2 + X3 <=10
Resolvendo pelo método gráfico, encontramos (2,5 , 2,5)
Então
Z= 3*0 + 7*2,5 + 5*2,5 = 30
Quando mudamos o valor do coeficiente de X1 na FO chega uma hora em que ficará mais vantajoso produzir apenas X1.
Zerando X2 e X3 (5,0,0)
30 = Alfa*5 + 7*0 + 5*0
Alfa = 6
69
Considere o seguinte problema
de programação linear:
Maximize: Z = x1 + 4x2
Sujeito a
2x1 + 4x2≤20
−x1 + 2x2≤8
x1 + x2≤5
x1≥0
x2≥0
Verifica-se que o valor ótimo
da função objetivo é
(A) 0 (B) 9 (C)
17 (D) 18 (E) 20
Tem que fazer um gráfico com
as três restrições, substituindo (1,0) e (0,1) em cada uma das restrições, aí
encontra dois ponto para traçar cada reta. Ex: ao substituir (1,0) na restrição
−x1 + 2x2=8, obtivemos (-8,0); ao substituir (0,1) na mesma restrição,
obtivemos (0,4), com esses dois pontos, traçamos a reta. Repare que 2x1 + 4x2 é
inútil.
Uma vez feito o gráfico,
lembramos que a solução ótima é o vértice (seta vermelha apontando para o
ponto) e para calcular o vértice (que é a intersecção de duas retas),
resolvemos o sistema:
x1 + x2 = 5
−x1 + 2x2 = 8
X1 = 2/3 e X2 = 13/3 à esta é a solução ótima. Para calcular Z, basta
substituir: Z= (2/3) + 4. (13/3) = 18. Alt D
Petrobras Distribuidora (a prova mais difícil de eng. de prod. que encontrei)
2011
63
De maneira geral, afirma-se
que aos problemas de maximização de programação linear na forma-padrão, corresponde
um problema de minimização denominado Problema Dual. Buscando obter as relações
entre o Problema Primal e o Problema Dual, sabe-se que
(A) o número de restrições do
Dual é igual ao número de restrições do Primal.
(B) o Dual do Primal é o
Primal.
(C) a matriz dos coeficientes
do Dual é a inversa da matriz dos coeficientes do Primal.
(D) se tanto o Primal quanto o
Dual tiverem soluções compatíveis finitas, então existe uma solução ótima
finita para cada um dos problemas, tal que o valor da função objetiva é igual
para os dois problemas.
(E) se um dos problemas não
tiver solução viável, então o outro terá soluções viáveis ou soluções ilimitadas.
Resolução
Não sei. Disseram nos comentário "primal e dual tem resposta iguais" Alt D.
IBGE
2009
54
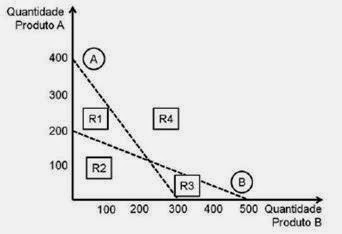
O gráfico acima
apresenta a solução gráfica de um problema de programação linear. Ele
representa as quantidades máximas de produção de dois itens do portfólio de uma
empresa. A linha A representa as restrições operacionais dos dois itens no
departamento de montagem e a linha B, as restrições do departamento de
embalagem da empresa. As regiões demarcadas entre as linhas tracejadas com
(B) R2
referem-se à capacidade viável dos dois itens produzidos na montagem e na
embalagem.
(C) R1 e R2
referem-se à capacidade mínina dos dois itens produzidos na na embalagem.
(D) R2 e R3
referem-se à capacidade mínina dos dois itens
produzidos na
montagem.
(E) R4
referem-se à capacidade viável dos dois itens produzidos na montagem e na
embalagem.
Resolução
O gráfico apresenta a parte
viável (porque atende às restrições) e a parte inviável (tudo que não é viável,
porque não atende a todas restrições). R2 é viável. R1 está dentro das
restrições de montagem, mas fora das restrições de embalagem, então é inviável.
R3 está dentro da embalagem, mas fora da montagem, também inviável. R4 está
fora de tudo, inviável.Alt B.